通用简谐梯形组合凸轮曲线设计的 Python 实现

发表于 | 分类于 | 阅读次数
本文基于通用简谐梯形组合凸轮曲线的加速度函数（$A$）对该曲线的设计原理进行探究，建立其速度函数（$V$）、位移函数（$S$）、跃度函数（$J$）、跳度函数（$Q$）的通用表达式，设置边界条件建立方程组并借助 sympy 对方程未知量进行求解，开发出可任意指定 $T_i$ 值并进行凸轮曲线设计的程序，借助 matplotlib 和 numpy 分别绘制出指定了 $T_i$ 值的推程、回程凸轮曲线及完整的凸轮位移运动曲线，并得到曲线特性值。

在凸轮机构的设计中，凸轮轮廓的形状主要取决于从动件的输出运动规律。描述这种运动规律的曲线被称为凸轮曲线。选择不同的凸轮曲线会对机构的运动和动力特性产生较大影响。在凸轮机构从动件推动负载运动的过程中，为了满足运动时间短、平稳、顺滑、无振动、耗能少的要求，首先需要解决如何设计和选择合适的凸轮曲线这个问题。

通用简谐梯形组合凸轮曲线具有良好的性能和较强的通用性，通过选择不同的分值区间 $T_i$ 就能得到绝大多数的基本运动规律和常用运动规律。它是由简谐曲线和梯形曲线组合而成的，因此兼有简谐运动规律在两端连续及梯形运动规律最大加速度较小的优点，是目前工程上应用很广的一种凸轮曲线，能够满足大多数中高速凸轮机构的设计要求。

曲线的函数表达式

查阅文献，已知通用简谐梯形组合凸轮曲线的加速度函数（$A$）为：

\[A = \left\{ \begin{array}{l} A_{mp}sinP_i & T\in[0,\ T_1]\\ A_{mp} & T\in(T_1,\ T_2]\\ A_{mp}cosP_i & T\in(T_2,\ T_3]\\ 0 & T\in(T_3,\ T_4]\\ -A_{mm}sinP_i & T\in(T_4,\ T_5]\\ -A_{mm} & T\in(T_5,\ T_6]\\ -A_{mm}cosP_i & T\in(T_6,\ 1] \end{array} \right.\]

其中，

\[P_i = \Big[(T - T_{i-1})/F_i + (i - 1)\frac{\pi}{4}\Big]\] \[F_i = (T_i - T_{i - 1})\Big/\frac{\pi}{2}\] \[0 \leq T_1 \leq T_2 \leq T_3 \leq T_4 \leq T_5 \leq T_6 \leq 1\]

根据

\[\left\{ \begin{array}{l} V = \frac{dS}{dT}\\ A = \frac{d^2S}{dT^2}\\ J = \frac{d^3S}{dT^3}\\ Q = AV\\ \end{array} \right.\]

可分别计算出速度函数（$V$）、位移函数（$S$）、跃度函数（$J$）、跳度函数（$Q$）的函数表达式，计算过程如下：

首先，导入所使用的模块：

1
2
from sympy import *
init_printing()

定义符号变量：

1
2
3
4
T, Amp, Amm = symbols('T, Amp, Amm', nonnegative=True)
T1, T2, T3, T4, T5, T6 = symbols('T1, T2, T3, T4, T5, T6', nonnegative=True, reals=True, infinite=False)
C1, C2, C3, C4, C5, C6, C7 = symbols('C1, C2, C3, C4, C5, C6, C7')
B1, B2, B3, B4, B5, B6, B7 = symbols('B1, B2, B3, B4, B5, B6, B7')

使用列表作为容器，放置各类函数表达式：

1
2
3
4
5
6
7
8
9
10
T_list = [0, T1, T2, T3, T4, T5, T6, 1]
C_list = [C1, C2, C3, C4, C5, C6, C7]
B_list = [B1, B2, B3, B4, B5, B6, B7]
F_list = []
P_list = []
A_list = []
J_list = []
V_list = []
S_list = []
Q_list = []

使用 sympy 对函数表达式进行计算，并将结果存储在已定义的列表中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
for i in range(1, len(T_list)):
    
    F_list.append((T_list[i] - T_list[i - 1])/(pi/2))
    P_list.append((T - T_list[i - 1])/F_list[i - 1] + (i - 1)*(pi/4))
    
    if i == 1 or i == 3:
        A_list.append(Amp*sin(P_list[i - 1]))
    elif i == 2:
        A_list.append(Amp)
    elif i == 4:
        A_list.append(0)
    elif i == 5 or i == 7:
        A_list.append(Amm*sin(P_list[i - 1]))
    else:
        A_list.append(-Amm)
    
    J_list.append(simplify(diff(A_list[i - 1], T)))
    
    if i == 1:
        V_list.append(simplify(Amp*(-2*T1/pi)*cos(pi*T/(2*T1)) + C_list[i - 1]))
    else:
        V_list.append(simplify(integrate(A_list[i - 1], T) + C_list[i - 1]))
    
    if i == 1:
        S_list.append(simplify(- 2*Amp*T1*(2*T1*sin(pi*T/(2*T1)))/pi/pi + B_list[i - 1] + C_list[i - 1]*T))
    else:
        S_list.append(simplify(integrate(V_list[i - 1], T) + B_list[i - 1]))
    
    Q_list.append(simplify(A_list[i - 1]*V_list[i - 1]))

为了便于书写及调用，定义以 $i$ 值为自变量并返回对应表达式的函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def A(i):
    return A_list[i - 1]

def V(i):
    return V_list[i - 1]
  
def S(i):
    return S_list[i - 1]

def J(i):
    return J_list[i - 1]
  
def Q(i):
    return Q_list[i - 1]

计算完毕后，分别查看 V(1) ~ V(7) 的返回值，得到：

\[V = \left\{ \begin{array}{l} - \frac{2 Amp}{\pi} T_{1} \cos{\left (\frac{\pi T}{2 T_{1}} \right )} + C_{1} & T\in[0,\ T_1]\\ Amp T + C_{2} & T\in(T_1,\ T_2]\\ \frac{1}{\pi} \left(2 Amp \left(T_{2} - T_{3}\right) \sin{\left (\frac{\pi \left(T - T_{2}\right)}{2 \left(T_{2} - T_{3}\right)} \right )} + \pi C_{3}\right) & T\in(T_2,\ T_3]\\ C_{4} & T\in(T_3,\ T_4]\\ \frac{1}{\pi} \left(- 2 Amm \left(T_{4} - T_{5}\right) \cos{\left (\frac{\pi \left(T - T_{4}\right)}{2 \left(T_{4} - T_{5}\right)} \right )} + \pi C_{5}\right) & T\in(T_4,\ T_5]\\ - Amm T + C_{6} & T\in(T_5,\ T_6]\\ \frac{1}{\pi} \left(- 2 Amm \left(T_{6} - 1\right) \sin{\left (\frac{\pi \left(T - T_{6}\right)}{2 \left(T_{6} - 1\right)} \right )} + \pi C_{7}\right) & T\in(T_6,\ 1] \end{array} \right.\]

分别查看 S(1) ~ S(7) 的返回值，得到：

\[S = \left\{ \begin{array}{l} - \frac{4 Amp}{\pi^{2}} T_{1}^{2} \sin{\left (\frac{\pi T}{2 T_{1}} \right )} + B_{1} + C_{1} T & T\in[0,\ T_1]\\ \frac{Amp T^{2}}{2} + B_{2} + C_{2} T & T\in(T_1,\ T_2]\\ \frac{1}{\pi^{2}} \left(- 4 Amp \left(T_{2} - T_{3}\right)^{2} \cos{\left (\frac{\pi \left(T - T_{2}\right)}{2 \left(T_{2} - T_{3}\right)} \right )} + \pi^{2} B_{3} + \pi^{2} C_{3} T\right) & T\in(T_2,\ T_3]\\ B_{4} + C_{4} T & T\in(T_3,\ T_4]\\ \frac{1}{\pi^{2}} \left(- 4 Amm \left(T_{4} - T_{5}\right)^{2} \sin{\left (\frac{\pi \left(T - T_{4}\right)}{2 \left(T_{4} - T_{5}\right)} \right )} + \pi^{2} B_{5} + \pi^{2} C_{5} T\right) & T\in(T_4,\ T_5]\\ - \frac{Amm T^{2}}{2} + B_{6} + C_{6} T & T\in(T_5,\ T_6]\\ \frac{1}{\pi^{2}} \left(4 Amm \left(T_{6} - 1\right)^{2} \cos{\left (\frac{\pi \left(T - T_{6}\right)}{2 \left(T_{6} - 1\right)} \right )} + \pi^{2} B_{7} + \pi^{2} C_{7} T\right) & T\in(T_6,\ 1] \end{array} \right.\]

分别查看 J(1) ~ J(7) 的返回值，得到：

\[J = \left\{ \begin{array}{l} \frac{\pi Amp}{2 T_{1}} \cos{\left (\frac{\pi T}{2 T_{1}} \right )} & T\in[0,\ T_1]\\ 0 & T\in(T_1,\ T_2]\\ - \frac{\pi Amp}{2 T_{2} - 2 T_{3}} \sin{\left (\frac{\pi \left(T - T_{2}\right)}{2 \left(T_{2} - T_{3}\right)} \right )} & T\in(T_2,\ T_3]\\ 0 & T\in(T_3,\ T_4]\\ \frac{\pi Amm}{2 \left(T_{4} - T_{5}\right)} \cos{\left (\frac{\pi \left(T - T_{4}\right)}{2 \left(T_{4} - T_{5}\right)} \right )} & T\in(T_4,\ T_5]\\ 0 & T\in(T_5,\ T_6]\\ \frac{\pi Amm}{2 \left(T_{6} - 1\right)} \sin{\left (\frac{\pi \left(T - T_{6}\right)}{2 \left(T_{6} - 1\right)} \right )} & T\in(T_6,\ 1] \end{array} \right.\]

分别查看 Q(1) ~ Q(7) 的返回值，得到：

\[Q = \left\{ \begin{array}{l} - \frac{Amp^{2} T_{1}}{\pi} \sin{\left (\frac{\pi T}{T_{1}} \right )} + Amp C_{1} \sin{\left (\frac{\pi T}{2 T_{1}} \right )} & T\in[0,\ T_1]\\ Amp \left(Amp T + C_{2}\right) & T\in(T_1,\ T_2]\\ \frac{Amp}{\pi} \left(2 Amp \left(T_{2} - T_{3}\right) \sin{\left (\frac{\pi \left(T - T_{2}\right)}{2 \left(T_{2} - T_{3}\right)} \right )} + \pi C_{3}\right) \cos{\left (\frac{\pi \left(T - T_{2}\right)}{2 \left(T_{2} - T_{3}\right)} \right )} & T\in(T_2,\ T_3]\\ 0 & T\in(T_3,\ T_4]\\ - \frac{Amm}{\pi} \left(2 Amm \left(T_{4} - T_{5}\right) \cos{\left (\frac{\pi \left(T - T_{4}\right)}{2 \left(T_{4} - T_{5}\right)} \right )} - \pi C_{5}\right) \sin{\left (\frac{\pi \left(T - T_{4}\right)}{2 \left(T_{4} - T_{5}\right)} \right )} & T\in(T_4,\ T_5]\\ Amm \left(Amm T - C_{6}\right) & T\in(T_5,\ T_6]\\ \frac{Amm}{\pi} \left(2 Amm \left(T_{6} - 1\right) \sin{\left (\frac{\pi \left(T - T_{6}\right)}{2 \left(T_{6} - 1\right)} \right )} - \pi C_{7}\right) \cos{\left (\frac{\pi \left(T - T_{6}\right)}{2 \left(T_{6} - 1\right)} \right )} & T\in(T_6,\ 1] \end{array} \right.\]

求解函数的未知常量

分别将上述 7 个区间的各函数命名为 $A_1$、$A_2$ …… $A_7$，$V_1$、$V_2$……$V_7$ 等。

在凸轮运动的推程阶段，速度和位移初始及末端的边界条件为：

\[\left\{ \begin{array}{l} V_1(0) = 0\\ V_7(1) = 0\\ S_1(0) = 0\\ S_7(1) = 1 \end{array} \right.\]

据此，可建立 4 个方程：

1
2
3
4
cond_1 = V(1).subs(T, T_list[0]) - 0
cond_2 = V(7).subs(T, T_list[7]) - 0
cond_3 = S(1).subs(T, T_list[0]) - 0
cond_4 = S(7).subs(T, T_list[7]) - 1

又因为在 $T_1$ 、$T_2$ 、$T_3$ 、$T_4$ 、$T_5$ 、$T_6$ 处，速度和位移具有连续性，即：

\[\left\{ \begin{array}{l} V_1(T_1) = V_2(T_1)\\ V_2(T_2) = V_3(T_2)\\ V_3(T_3) = V_4(T_3)\\ V_4(T_4) = V_5(T_4)\\ V_5(T_5) = V_6(T_5)\\ V_6(T_6) = V_7(T_6)\\ S_1(T_1) = S_2(T_1)\\ S_2(T_2) = S_3(T_2)\\ S_3(T_3) = S_4(T_3)\\ S_4(T_4) = S_5(T_4)\\ S_5(T_5) = S_6(T_5)\\ S_6(T_6) = S_7(T_6) \end{array} \right.\]

据此，可建立 12 个方程：

1
2
3
4
5
6
7
8
9
10
11
12
cond_5 = V(1).subs(T, T_list[1]) - V(2).subs(T, T_list[1])
cond_6 = V(2).subs(T, T_list[2]) - V(3).subs(T, T_list[2])
cond_7 = V(3).subs(T, T_list[3]) - V(4).subs(T, T_list[3])
cond_8 = V(4).subs(T, T_list[4]) - V(5).subs(T, T_list[4])
cond_9 = V(5).subs(T, T_list[5]) - V(6).subs(T, T_list[5])
cond_10 = V(6).subs(T, T_list[6]) - V(7).subs(T, T_list[6])
cond_11 = S(1).subs(T, T_list[1]) - S(2).subs(T, T_list[1])
cond_12 = S(2).subs(T, T_list[2]) - S(3).subs(T, T_list[2])
cond_13 = S(3).subs(T, T_list[3]) - S(4).subs(T, T_list[3])
cond_14 = S(4).subs(T, T_list[4]) - S(5).subs(T, T_list[4])
cond_15 = S(5).subs(T, T_list[5]) - S(6).subs(T, T_list[5])
cond_16 = S(6).subs(T, T_list[6]) - S(7).subs(T, T_list[6])

联立上述 16 个方程，使用 sympy 的 nonlinsolve 函数求解该十六元非线性方程组，得到 $C_1$ ~ $C_7$、$B_1$ ~ $B_7$ 以及 $A_{mp}$、$A_{mm}$ 的符号表达式：

1
roots = nonlinsolve([cond_1, cond_2, cond_3, cond_4, cond_5, cond_6, cond_7, cond_8, cond_9, cond_10, cond_11, cond_12, cond_13, cond_14, cond_15, cond_16],   (C1, C2, C3, C4, C5, C6, C7, B1, B2, B3, B4, B5, B6, B7, Amp, Amm))

在输出求解结果后，发现这些常量的表达式含有一个共同的因子，故先将其单独提出来以简化表达式：

\[D = - 16 T_{1}^{2} T_{4} + 2 \pi^{2} T_{1}^{2} T_{4} - 8 \pi T_{1}^{2} T_{5} - 2 \pi^{2} T_{1}^{2} T_{5} + 16 T_{1}^{2} T_{5} + \pi^{3} T_{1}^{2} T_{5} - \pi^{3} T_{1}^{2} T_{6} - \\ 16 T_{1}^{2} T_{6} + 2 \pi^{2} T_{1}^{2} T_{6} + 8 \pi T_{1}^{2} T_{6} - 2 \pi^{2} T_{1}^{2} + 16 T_{1}^{2} - 4 \pi^{2} T_{1} T_{4}^{2} - 16 T_{1} T_{4}^{2} + 16 \pi T_{1} T_{4}^{2} - \\ 24 \pi T_{1} T_{4} T_{5} + 32 T_{1} T_{4} T_{5} + 4 \pi^{2} T_{1} T_{4} T_{5} - \pi^{3} T_{1} T_{5}^{2} - 16 T_{1} T_{5}^{2} + 2 \pi^{2} T_{1} T_{5}^{2} + 8 \pi T_{1} T_{5}^{2} - \\ 8 \pi T_{1} T_{6}^{2} - 2 \pi^{2} T_{1} T_{6}^{2} + 16 T_{1} T_{6}^{2} + \pi^{3} T_{1} T_{6}^{2} - 4 \pi^{2} T_{1} T_{6} - 32 T_{1} T_{6} + 24 \pi T_{1} T_{6} - 16 \pi T_{1} + 16 T_{1} + \\ 4 \pi^{2} T_{1} - 2 \pi^{2} T_{2}^{2} T_{4} + 16 T_{2}^{2} T_{4} - \pi^{3} T_{2}^{2} T_{5} - 16 T_{2}^{2} T_{5} + 2 \pi^{2} T_{2}^{2} T_{5} + 8 \pi T_{2}^{2} T_{5} - 8 \pi T_{2}^{2} T_{6} - \\ 2 \pi^{2} T_{2}^{2} T_{6} + 16 T_{2}^{2} T_{6} + \pi^{3} T_{2}^{2} T_{6} - 16 T_{2}^{2} + 2 \pi^{2} T_{2}^{2} - 32 T_{2} T_{3} T_{4} + 8 \pi T_{2} T_{3} T_{4} - 24 \pi T_{2} T_{3} T_{5} + \\ 32 T_{2} T_{3} T_{5} + 4 \pi^{2} T_{2} T_{3} T_{5} - 4 \pi^{2} T_{2} T_{3} T_{6} - 32 T_{2} T_{3} T_{6} + 24 \pi T_{2} T_{3} T_{6} - 8 \pi T_{2} T_{3} + 32 T_{2} T_{3} - \\ 16 \pi T_{2} T_{4}^{2} + 16 T_{2} T_{4}^{2} + 4 \pi^{2} T_{2} T_{4}^{2} - 4 \pi^{2} T_{2} T_{4} T_{5} - 32 T_{2} T_{4} T_{5} + 24 \pi T_{2} T_{4} T_{5} - 8 \pi T_{2} T_{5}^{2} - \\ 2 \pi^{2} T_{2} T_{5}^{2} + 16 T_{2} T_{5}^{2} + \pi^{3} T_{2} T_{5}^{2} - \pi^{3} T_{2} T_{6}^{2} - 16 T_{2} T_{6}^{2} + 2 \pi^{2} T_{2} T_{6}^{2} + 8 \pi T_{2} T_{6}^{2} - 24 \pi T_{2} T_{6} + \\ 32 T_{2} T_{6} + 4 \pi^{2} T_{2} T_{6} - 4 \pi^{2} T_{2} - 16 T_{2} + 16 \pi T_{2} - 8 \pi T_{3}^{2} T_{4} + 16 T_{3}^{2} T_{4} - 4 \pi^{2} T_{3}^{2} T_{5} - 16 T_{3}^{2} T_{5} + \\ 16 \pi T_{3}^{2} T_{5} - 16 \pi T_{3}^{2} T_{6} + 16 T_{3}^{2} T_{6} + 4 \pi^{2} T_{3}^{2} T_{6} - 16 T_{3}^{2} + 8 \pi T_{3}^{2} - 16 T_{3} T_{4}^{2} + 8 \pi T_{3} T_{4}^{2} - 8 \pi T_{3} T_{4} T_{5} + \\ 32 T_{3} T_{4} T_{5} - 16 T_{3} T_{5}^{2} + 2 \pi^{2} T_{3} T_{5}^{2} - 2 \pi^{2} T_{3} T_{6}^{2} + 16 T_{3} T_{6}^{2} - 32 T_{3} T_{6} + 8 \pi T_{3} T_{6} - 8 \pi T_{3} + 16 T_{3}\]

于是，可以得到方程组的解如下：

\[\left\{ \begin{array}{l} C_1 = \frac{4 \pi}{D} T_{1} \left(2 T_{4} - 2 T_{5} + \pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right)\\ C_2 = - \frac{2 \pi}{D} T_{1} \left(-2 + \pi\right) \left(2 T_{4} - 2 T_{5} + \pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right)\\ C_3 = - \frac{2 \pi}{D} \left(- 2 T_{1} + \pi T_{1} - \pi T_{2}\right) \left(2 T_{4} - 2 T_{5} + \pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right)\\ C_4 = - \frac{2 \pi}{D} \left(- 2 T_{1} + \pi T_{1} - \pi T_{2} + 2 T_{2} - 2 T_{3}\right) \left(2 T_{4} - 2 T_{5} + \pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right)\\ C_5 = - \frac{2 \pi}{D} \left(\pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right) \left(- 2 T_{1} + \pi T_{1} - \pi T_{2} + 2 T_{2} - 2 T_{3}\right)\\ C_6 = \frac{2 \pi}{D} \left(- 2 T_{6} + \pi T_{6} + 2\right) \left(- 2 T_{1} + \pi T_{1} - \pi T_{2} + 2 T_{2} - 2 T_{3}\right)\\ C_7 = - \frac{4 \pi}{D} \left(T_{6} - 1\right) \left(- 2 T_{1} + \pi T_{1} - \pi T_{2} + 2 T_{2} - 2 T_{3}\right)\\ B_1 = 0\\ B_2 = \frac{T_{1}^{2}}{D} \left(-8 + \pi^{2}\right) \left(2 T_{4} - 2 T_{5} + \pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right)\\ B_3 = \frac{1}{D} \left(- 8 T_{1}^{2} + \pi^{2} T_{1}^{2} - \pi^{2} T_{2}^{2} + 8 T_{2}^{2} - 16 T_{2} T_{3} + 8 T_{3}^{2}\right) \left(2 T_{4} - 2 T_{5} + \pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right)\\ B_4 = \frac{1}{D} \left(2 T_{4} - 2 T_{5} + \pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right) \left(- 8 T_{1}^{2} + \pi^{2} T_{1}^{2} - \pi^{2} T_{2}^{2} + 8 T_{2}^{2} - 16 T_{2} T_{3} + 4 \pi T_{2} T_{3} - 4 \pi T_{3}^{2} + 8 T_{3}^{2}\right)\\ B_5 = \frac{1}{D} \left(- 16 T_{1}^{2} T_{4} + 2 \pi^{2} T_{1}^{2} T_{4} - 8 \pi T_{1}^{2} T_{5} - 2 \pi^{2} T_{1}^{2} T_{5} + 16 T_{1}^{2} T_{5} + \pi^{3} T_{1}^{2} T_{5} - \pi^{3} T_{1}^{2} T_{6} - 16 T_{1}^{2} T_{6} + 2 \pi^{2} T_{1}^{2} T_{6} + \\ \qquad 8 \pi T_{1}^{2} T_{6} - 2 \pi^{2} T_{1}^{2} + 16 T_{1}^{2} - 4 \pi^{2} T_{1} T_{4}^{2} + 8 \pi T_{1} T_{4}^{2} - 8 \pi T_{1} T_{4} T_{5} + 4 \pi^{2} T_{1} T_{4} T_{5} - 2 \pi^{2} T_{2}^{2} T_{4} + 16 T_{2}^{2} T_{4} - \\ \qquad \pi^{3} T_{2}^{2} T_{5} - 16 T_{2}^{2} T_{5} + 2 \pi^{2} T_{2}^{2} T_{5} + 8 \pi T_{2}^{2} T_{5} - 8 \pi T_{2}^{2} T_{6} - 2 \pi^{2} T_{2}^{2} T_{6} + 16 T_{2}^{2} T_{6} + \pi^{3} T_{2}^{2} T_{6} - 16 T_{2}^{2} + 2 \pi^{2} T_{2}^{2} - \\ \qquad 32 T_{2} T_{3} T_{4} + 8 \pi T_{2} T_{3} T_{4} - 24 \pi T_{2} T_{3} T_{5} + 32 T_{2} T_{3} T_{5} + 4 \pi^{2} T_{2} T_{3} T_{5} - 4 \pi^{2} T_{2} T_{3} T_{6} - 32 T_{2} T_{3} T_{6} + 24 \pi T_{2} T_{3} T_{6} - \\ \qquad 8 \pi T_{2} T_{3} + 32 T_{2} T_{3} - 8 \pi T_{2} T_{4}^{2} + 4 \pi^{2} T_{2} T_{4}^{2} - 4 \pi^{2} T_{2} T_{4} T_{5} + 8 \pi T_{2} T_{4} T_{5} - 8 \pi T_{3}^{2} T_{4} + 16 T_{3}^{2} T_{4} - 4 \pi^{2} T_{3}^{2} T_{5} - \\ \qquad 16 T_{3}^{2} T_{5} + 16 \pi T_{3}^{2} T_{5} - 16 \pi T_{3}^{2} T_{6} + 16 T_{3}^{2} T_{6} + 4 \pi^{2} T_{3}^{2} T_{6} - 16 T_{3}^{2} + 8 \pi T_{3}^{2} + 8 \pi T_{3} T_{4}^{2} - 8 \pi T_{3} T_{4} T_{5}\right)\\ B_6 = \frac{1}{D} \left(- 16 T_{1}^{2} T_{4} + 2 \pi^{2} T_{1}^{2} T_{4} - 8 \pi T_{1}^{2} T_{5} - 2 \pi^{2} T_{1}^{2} T_{5} + 16 T_{1}^{2} T_{5} + \pi^{3} T_{1}^{2} T_{5} - \pi^{3} T_{1}^{2} T_{6} - 16 T_{1}^{2} T_{6} + 2 \pi^{2} T_{1}^{2} T_{6} + \\ \qquad 8 \pi T_{1}^{2} T_{6} - 2 \pi^{2} T_{1}^{2} + 16 T_{1}^{2} - 4 \pi^{2} T_{1} T_{4}^{2} - 16 T_{1} T_{4}^{2} + 16 \pi T_{1} T_{4}^{2} - 24 \pi T_{1} T_{4} T_{5} + 32 T_{1} T_{4} T_{5} + 4 \pi^{2} T_{1} T_{4} T_{5} - \\ \qquad \pi^{3} T_{1} T_{5}^{2} - 16 T_{1} T_{5}^{2} + 2 \pi^{2} T_{1} T_{5}^{2} + 8 \pi T_{1} T_{5}^{2} - 2 \pi^{2} T_{2}^{2} T_{4} + 16 T_{2}^{2} T_{4} - \pi^{3} T_{2}^{2} T_{5} - 16 T_{2}^{2} T_{5} + 2 \pi^{2} T_{2}^{2} T_{5} + \\ \qquad 8 \pi T_{2}^{2} T_{5} - 8 \pi T_{2}^{2} T_{6} - 2 \pi^{2} T_{2}^{2} T_{6} + 16 T_{2}^{2} T_{6} + \pi^{3} T_{2}^{2} T_{6} - 16 T_{2}^{2} + 2 \pi^{2} T_{2}^{2} - 32 T_{2} T_{3} T_{4} + 8 \pi T_{2} T_{3} T_{4} - \\ \qquad 24 \pi T_{2} T_{3} T_{5} + 32 T_{2} T_{3} T_{5} + 4 \pi^{2} T_{2} T_{3} T_{5} - 4 \pi^{2} T_{2} T_{3} T_{6} - 32 T_{2} T_{3} T_{6} + 24 \pi T_{2} T_{3} T_{6} - 8 \pi T_{2} T_{3} + 32 T_{2} T_{3} - \\ \qquad 16 \pi T_{2} T_{4}^{2} + 16 T_{2} T_{4}^{2} + 4 \pi^{2} T_{2} T_{4}^{2} - 4 \pi^{2} T_{2} T_{4} T_{5} - 32 T_{2} T_{4} T_{5} + 24 \pi T_{2} T_{4} T_{5} - 8 \pi T_{2} T_{5}^{2} - 2 \pi^{2} T_{2} T_{5}^{2} + \\ \qquad 16 T_{2} T_{5}^{2} + \pi^{3} T_{2} T_{5}^{2} - 8 \pi T_{3}^{2} T_{4} + 16 T_{3}^{2} T_{4} - 4 \pi^{2} T_{3}^{2} T_{5} - 16 T_{3}^{2} T_{5} + 16 \pi T_{3}^{2} T_{5} - 16 \pi T_{3}^{2} T_{6} + 16 T_{3}^{2} T_{6} + \\ \qquad 4 \pi^{2} T_{3}^{2} T_{6} - 16 T_{3}^{2} + 8 \pi T_{3}^{2} - 16 T_{3} T_{4}^{2} + 8 \pi T_{3} T_{4}^{2} - 8 \pi T_{3} T_{4} T_{5} + 32 T_{3} T_{4} T_{5} - 16 T_{3} T_{5}^{2} + 2 \pi^{2} T_{3} T_{5}^{2}\right)\\ B_7 = \frac{1}{D} \left(- 16 T_{1}^{2} T_{4} + 2 \pi^{2} T_{1}^{2} T_{4} - 8 \pi T_{1}^{2} T_{5} - 2 \pi^{2} T_{1}^{2} T_{5} + 16 T_{1}^{2} T_{5} + \pi^{3} T_{1}^{2} T_{5} - \pi^{3} T_{1}^{2} T_{6} - 16 T_{1}^{2} T_{6} + 2 \pi^{2} T_{1}^{2} T_{6} + \\ \qquad 8 \pi T_{1}^{2} T_{6} - 2 \pi^{2} T_{1}^{2} + 16 T_{1}^{2} - 4 \pi^{2} T_{1} T_{4}^{2} - 16 T_{1} T_{4}^{2} + 16 \pi T_{1} T_{4}^{2} - 24 \pi T_{1} T_{4} T_{5} + 32 T_{1} T_{4} T_{5} + 4 \pi^{2} T_{1} T_{4} T_{5} - \\ \qquad \pi^{3} T_{1} T_{5}^{2} - 16 T_{1} T_{5}^{2} + 2 \pi^{2} T_{1} T_{5}^{2} + 8 \pi T_{1} T_{5}^{2} - 8 \pi T_{1} T_{6}^{2} - 2 \pi^{2} T_{1} T_{6}^{2} + 16 T_{1} T_{6}^{2} + \pi^{3} T_{1} T_{6}^{2} - 32 T_{1} T_{6} + \\ \qquad 16 \pi T_{1} T_{6} - 8 \pi T_{1} + 16 T_{1} - 2 \pi^{2} T_{2}^{2} T_{4} + 16 T_{2}^{2} T_{4} - \pi^{3} T_{2}^{2} T_{5} - 16 T_{2}^{2} T_{5} + 2 \pi^{2} T_{2}^{2} T_{5} + 8 \pi T_{2}^{2} T_{5} - 8 \pi T_{2}^{2} T_{6} - \\ \qquad 2 \pi^{2} T_{2}^{2} T_{6} + 16 T_{2}^{2} T_{6} + \pi^{3} T_{2}^{2} T_{6} - 16 T_{2}^{2} + 2 \pi^{2} T_{2}^{2} - 32 T_{2} T_{3} T_{4} + 8 \pi T_{2} T_{3} T_{4} - 24 \pi T_{2} T_{3} T_{5} + 32 T_{2} T_{3} T_{5} + \\ \qquad 4 \pi^{2} T_{2} T_{3} T_{5} - 4 \pi^{2} T_{2} T_{3} T_{6} - 32 T_{2} T_{3} T_{6} + 24 \pi T_{2} T_{3} T_{6} - 8 \pi T_{2} T_{3} + 32 T_{2} T_{3} - 16 \pi T_{2} T_{4}^{2} + 16 T_{2} T_{4}^{2} + \\ \qquad 4 \pi^{2} T_{2} T_{4}^{2} - 4 \pi^{2} T_{2} T_{4} T_{5} - 32 T_{2} T_{4} T_{5} + 24 \pi T_{2} T_{4} T_{5} - 8 \pi T_{2} T_{5}^{2} - 2 \pi^{2} T_{2} T_{5}^{2} + 16 T_{2} T_{5}^{2} + \pi^{3} T_{2} T_{5}^{2} - \\ \qquad \pi^{3} T_{2} T_{6}^{2} - 16 T_{2} T_{6}^{2} + 2 \pi^{2} T_{2} T_{6}^{2} + 8 \pi T_{2} T_{6}^{2} - 16 \pi T_{2} T_{6} + 32 T_{2} T_{6} - 16 T_{2} + 8 \pi T_{2} - 8 \pi T_{3}^{2} T_{4} + 16 T_{3}^{2} T_{4} - \\ \qquad 4 \pi^{2} T_{3}^{2} T_{5} - 16 T_{3}^{2} T_{5} + 16 \pi T_{3}^{2} T_{5} - 16 \pi T_{3}^{2} T_{6} + 16 T_{3}^{2} T_{6} + 4 \pi^{2} T_{3}^{2} T_{6} - 16 T_{3}^{2} + 8 \pi T_{3}^{2} - 16 T_{3} T_{4}^{2} + 8 \pi T_{3} T_{4}^{2} - \\ \qquad 8 \pi T_{3} T_{4} T_{5} + 32 T_{3} T_{4} T_{5} - 16 T_{3} T_{5}^{2} + 2 \pi^{2} T_{3} T_{5}^{2} - 2 \pi^{2} T_{3} T_{6}^{2} + 16 T_{3} T_{6}^{2} - 32 T_{3} T_{6} + 16 T_{3}\right)\\ A_{mp} = \frac{2 \pi^{2}}{D} \left(2 T_{4} - 2 T_{5} + \pi T_{5} - \pi T_{6} + 2 T_{6} - 2\right)\\ A_{mm} = \frac{2 \pi^{2}}{D} \left(- 2 T_{1} + \pi T_{1} - \pi T_{2} + 2 T_{2} - 2 T_{3}\right) \end{array} \right.\]

完成这些常量未知数的求解后，给定任意的 $T_i$ 值，将其代入常量表达式中可以计算出常量的准确值，再将这些常量值代入到曲线函数中，即可得到在这些 $T_i$ 值条件下的准确曲线函数。

凸轮运动曲线设计

建立了一个常见凸轮运动曲线数据库，可供直接调用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
cam_library = {
    
    # 不连续曲线
    11: ([0, 0, 1/2, 1/2, 1/2, 1/2, 1, 1], '等加速度曲线'),
    12: ([0, 0, 0, 1/2, 1/2, 1, 1, 1], '余弦曲线'),
    
    # 双停留对称曲线
    22: ([0, 1/4, 1/4, 1/2, 1/2, 3/4, 3/4, 1], '摆线曲线'),
    25: ([0, 1/8, 3/8, 1/2, 1/2, 5/8, 7/8, 1], '修正梯形曲线'),
    26: ([0, 1/8, 1/8, 1/2, 1/2, 7/8, 7/8, 1], '修正正弦曲线'),
    27: ([0, 1/16, 1/16, 1/4, 3/4, 15/16, 15/16, 1], '修正等速曲线'),
    
    # 双停留非对称曲线
    1: ([0, 1/8, 3/8, 1/2, 1/2, 5/8, 5/8, 1], '梯形摆线曲线'), 
    33: ([0, 1/5, 1/5, 2/5, 2/5, 7/10, 7/10, 1], '非对称摆线曲线'),
    34: ([0, 1/10, 3/10, 2/5, 2/5, 11/20, 17/20, 1], '斜修正梯形曲线'),
    35: ([0, 0.125, 0.319492264824171, 0.444492264824171, 0.444492264824171, 0.569492264824171, 0.569492264824171, 1], '梯形摆线'),
    
    # 单停留曲线
    2: ([0, 0, 0, 1/2, 1/2, 3/4, 3/4, 1], '单停留摆线曲线'),
    3: ([0, 1/8, 3/8, 1/2, 1/2, 1, 1, 1], '单停留梯形摆线曲线'),
    43:([0, 0.25, 0.25, 0.5, 0.5, 1, 1, 1], '单停留摆线 m=1'),
    44:([0, 0.2, 0.2, 0.4, 0.4, 1, 1, 1], '单停留摆线 m=2/3'),
    45:([0, 0.125, 0.397711264227026, 0.522711264227026, 0.522711264227026, 0.647711264227026, 1, 1], '单停留修正梯形 m=1'),
    46: ([0, 1/8, 3/8, 1/2, 1/2, 5/8, 1, 1], '单停留修正梯形 Ferguson'),
    47:([0, 0.125, 0.317394359890449, 0.442394359890449, 0.442394359890449, 0.525727693223782, 1, 1], '单停留修正梯形 m=2/3'),
    48: ([0, 1/8, 1/8, 1/2, 1/2, 1, 1, 1], '单停留修正正弦曲线'),
    49: ([0, 0.125, 0.319492264824171, 0.444492264824171, 0.444492264824171, 1, 1, 1], '单停留梯形摆线'),
    
    # 无停留曲线
    51: ([0, 0, 1/4, 1/2, 1/2, 3/4, 1, 1], '无停留修正梯形曲线'),
    52: ([0, 0, 0, 1/4, 3/4, 1, 1, 1], '无停留修正等速曲线'),
    
    # 其他
    92: ([0, 0, 1/4, 1/3, 1/3, 5/6, 5/6, 1], 'NC2'),
}

通过以下代码指定凸轮的推程运动角、远休止角、回程运动角和近休止角：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np

phi, phi_s, phi_f, phi_c = symbols("phi, phi_s, phi^', phi_c")
phi_list = [90, 90, 90, 90]
phi_list[0] = int(input('输入推程运动角的值（默认为90°）：'))
phi_list[1] = int(input('输入远休止角的值（默认为90°）：'))
phi_list[2] = int(input('输入回程运动角的值（默认为90°）：'))
phi_list[3] = 360 - phi_list[0] - phi_list[1] - phi_list[2]

phi_1 = phi_list[0]
phi_2 = phi_list[0] + phi_list[1]
phi_3 = phi_list[0] + phi_list[1] + phi_list[2]

accur = 10

T_axis = np.array([])
A_axis = np.array([])
J_axis = np.array([])
V_axis = np.array([])
S_axis = np.array([])

T_axis_final = np.array([])
S_axis_final = np.array([])

定义推程运动曲线：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
T_value = [0, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1]
select_type = int(input('0--采用内置曲线库；1--自定义T值输入\n请输入：'))
if select_type == 0:
    select_curve = int(input('输入曲线代码：'))
    T_value = cam_library[select_curve][0]
    print('你选择了', cam_library[select_curve][1])
elif select_type == 1:
    print('依次指定 T1 ~ T6 的值，T0 = 0，T7 = 1')
    for i in range(1, 7):
        print('指定 T', i, '的值：')
        T_value[i] = float(input())
else:
    print('无效的输入，程序将使用预设T值[0, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1]')

curve_type = []
curve_type.append(cam_library[select_curve][1])

例如选择修正正弦曲线作为凸轮的推程运动曲线，代入 $T_i$ 值，计算常量的数值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
subs_list = [(T1, T_value[1]), (T2, T_value[2]), (T3, T_value[3]), (T4, T_value[4]), \
             (T5, T_value[5]), (T6, T_value[6]), (pi, 3.1415926535897932384626433832795)]

for i in range(len(C_list)):
        C_list[i] = roots_list[0][i].subs(subs_list)

subs_list.extend([(C1, C_list[0]), (C2, C_list[1]), (C3, C_list[2]), (C4, C_list[3]), \
                 (C5, C_list[4]), (C6, C_list[5]), (C7, C_list[6])])

for i in range(len(B_list)):
        B_list[i] = roots_list[0][i + 7].subs(subs_list)
    
subs_list.extend([(B1, B_list[0]), (B2, B_list[1]), (B3, B_list[2]), (B4, B_list[3]), \
                 (B5, B_list[4]), (B6, B_list[5]), (B7, B_list[6])])

Amp_Amm = [roots_list[0][-2].subs(subs_list), roots_list[0][-1].subs(subs_list)]
subs_list.extend([(Amp, Amp_Amm[0]), (Amm, Amp_Amm[1])])

代入常量值，得到准确的曲线函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
A_func = []
V_func = []
S_func = []
J_func = []

for i in range(1, len(T_value)):
    if i == 1 or i == 3 or i == 5 or i == 7:
        A_func.append(A(i).subs(subs_list))
    elif i == 2:
        A_func.append(Amp_Amm[0])
    elif i == 4:
        A_func.append(0)
    else:
        A_func.append(- Amp_Amm[1])
    
    if i % 2 == 0:
        J_func.append(0)
    else:
        J_func.append(J(i).subs(subs_list))
    
    V_func.append(V(i).subs(subs_list))
    S_func.append(S(i).subs(subs_list))

生成用于绘制曲线图像的点阵：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
step = phi_list[0]*accur
T_axis = np.linspace(0, 1, step, endpoint=False)

for i in range(1, len(T_value)):
    if T_value[i - 1] != T_value[i]:
        for j in range(len(T_axis)):
            
            if T_value[i - 1] <= T_axis[j] < T_value[i] or T_value[i] == T_axis[j] and T_axis[j] == 1:
                if i == 1 or i == 3:
                    A_axis = np.append(A_axis, A_func[i - 1].subs([(T, T_axis[j])]))
                elif i == 2:
                    A_axis = np.append(A_axis, Amp_Amm[0])
                elif i == 4:
                    A_axis = np.append(A_axis, 0)
                elif i == 5 or i == 7:
                    A_axis = np.append(A_axis, A_func[i - 1].subs([(T, T_axis[j])]))
                elif i == 6:
                    A_axis = np.append(A_axis, - Amp_Amm[1])
                
                if i % 2 == 0:
                    J_axis = np.append(J_axis, 0)
                else:
                    J_axis = np.append(J_axis, J_func[i - 1].subs([(T, T_axis[j])]))
                
                V_axis = np.append(V_axis, V_func[i - 1].subs([(T, T_axis[j])]))
                S_axis = np.append(S_axis, S_func[i - 1].subs([(T, T_axis[j])]))
            else:
                continue

Q_axis = np.multiply(A_axis, V_axis)

绘制曲线图像：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
import matplotlib.pyplot as plt

def plot_T_value():
    for i in range(len(T_value)):
        plt.axvline(x=T_value[i], ymin=0, ymax=1, color='k', linewidth=1, linestyle='--')

plt.plot(T_axis, S_axis, color='k')
if select_type == 0:
    plt.title(cam_library[select_curve][1] + '的位移曲线', fontproperties="SimHei", fontsize=14)
elif select_type == 1:
    plt.title('自定义曲线的位移曲线', fontproperties="SimHei", fontsize=14)
else:
    plt.title('默认曲线的位移曲线', fontproperties="SimHei", fontsize=14)
plt.xlabel('T',fontproperties='SimHei',fontsize=14)
plt.ylabel('S',fontproperties='SimHei',fontsize=14)
plot_T_value()
plt.xlim(0, 1)
plt.show()

plt.plot(T_axis, V_axis, color='k')
if select_type == 0:
    plt.title(cam_library[select_curve][1] + '的速度曲线', fontproperties="SimHei", fontsize=14)
elif select_type == 1:
    plt.title('自定义曲线的速度曲线', fontproperties="SimHei", fontsize=14)
else:
    plt.title('默认曲线的速度曲线', fontproperties="SimHei", fontsize=14)
plt.xlabel('T',fontproperties='SimHei',fontsize=14)
plt.ylabel('V',fontproperties='SimHei',fontsize=14)
plot_T_value()
plt.xlim(0, 1)
plt.scatter(T_axis[int(V_axis.argmax())], np.max(V_axis), s=40, color='k')
plt.text(T_axis[int(V_axis.argmax())] + 0.04, np.max(V_axis) + 0.01, r'$V_m$ = %.3f'%(np.max(V_axis)),
         fontdict={'size': 12, 'color': 'k'})
plt.show()

plt.plot(T_axis, A_axis, color='k')
if select_type == 0:
    plt.title(cam_library[select_curve][1] + '的加速度曲线', fontproperties="SimHei", fontsize=14)
elif select_type == 1:
    plt.title('自定义曲线的加速度曲线', fontproperties="SimHei", fontsize=14)
else:
    plt.title('默认曲线的加速度曲线', fontproperties="SimHei", fontsize=14)
plt.xlabel('T',fontproperties='SimHei',fontsize=14)
plt.ylabel('A',fontproperties='SimHei',fontsize=14)
plot_T_value()
plt.xlim(0, 1)
plt.scatter(T_axis[int(A_axis.argmax())], np.max(A_axis), s=40, color='k')
plt.text(T_axis[int(A_axis.argmax())] + 0.04, np.max(A_axis) - 0.7, r'$A_{mp}$ = %.3f'%(np.max(A_axis)),
         fontdict={'size': 12, 'color': 'k'})
plt.scatter(T_axis[int(A_axis.argmin())], np.min(A_axis), s=40, color='k')
plt.text(T_axis[int(A_axis.argmin())] - 0.32, np.min(A_axis) - 0.5, r'$A_{mm}$ = %.3f'%(np.min(A_axis)),
         fontdict={'size': 12, 'color': 'k'})
plt.show()

plt.plot(T_axis, J_axis, color='k')
if select_type == 0:
    plt.title(cam_library[select_curve][1] + '的跃度曲线', fontproperties="SimHei", fontsize=14)
elif select_type == 1:
    plt.title('自定义曲线的跃度曲线', fontproperties="SimHei", fontsize=14)
else:
    plt.title('默认曲线的跃度曲线', fontproperties="SimHei", fontsize=14)
plt.xlabel('T',fontproperties='SimHei',fontsize=14)
plt.ylabel('J',fontproperties='SimHei',fontsize=14)
plot_T_value()
plt.xlim(0, 1)
plt.scatter(T_axis[int(J_axis.argmax())], np.max(J_axis), s=40, color='k')
plt.text(T_axis[int(J_axis.argmax())] + 0.04, np.max(J_axis) + 0.02, r'$J_{max}$ = %.3f'%(np.max(J_axis)),
         fontdict={'size': 12, 'color': 'k'})
plt.scatter(T_axis[int(J_axis.argmin())], np.min(J_axis), s=40, color='k')
plt.text(T_axis[int(J_axis.argmin())] - 0.32, np.min(J_axis) - 0.5, r'$J_{min}$ = %.3f'%(np.min(J_axis)),
         fontdict={'size': 12, 'color': 'k'})
plt.show()

plt.plot(T_axis, Q_axis, color='k')
if select_type == 0:
    plt.title(cam_library[select_curve][1] + '的跳度曲线', fontproperties="SimHei", fontsize=14)
elif select_type == 1:
    plt.title('自定义曲线的跳度曲线', fontproperties="SimHei", fontsize=14)
else:
    plt.title('默认曲线的跳度曲线', fontproperties="SimHei", fontsize=14)
plt.xlabel('T',fontproperties='SimHei',fontsize=14)
plt.ylabel('Q',fontproperties='SimHei',fontsize=14)
plot_T_value()
plt.xlim(0, 1)
plt.scatter(T_axis[int(Q_axis.argmax())], np.max(Q_axis), s=40, color='k')
plt.text(T_axis[int(Q_axis.argmax())] + 0.04, np.max(Q_axis), r'$Q_{max}$ = %.3f'%(np.max(Q_axis)),
         fontdict={'size': 12, 'color': 'k'})
plt.scatter(T_axis[int(Q_axis.argmin())], np.min(Q_axis), s=40, color='k')
plt.text(T_axis[int(Q_axis.argmin())] - 0.32, np.min(Q_axis) - 0.5, r'$Q_{min}$ = %.3f'%(np.min(Q_axis)),
         fontdict={'size': 12, 'color': 'k'})
plt.show()

1

2

3

4

5

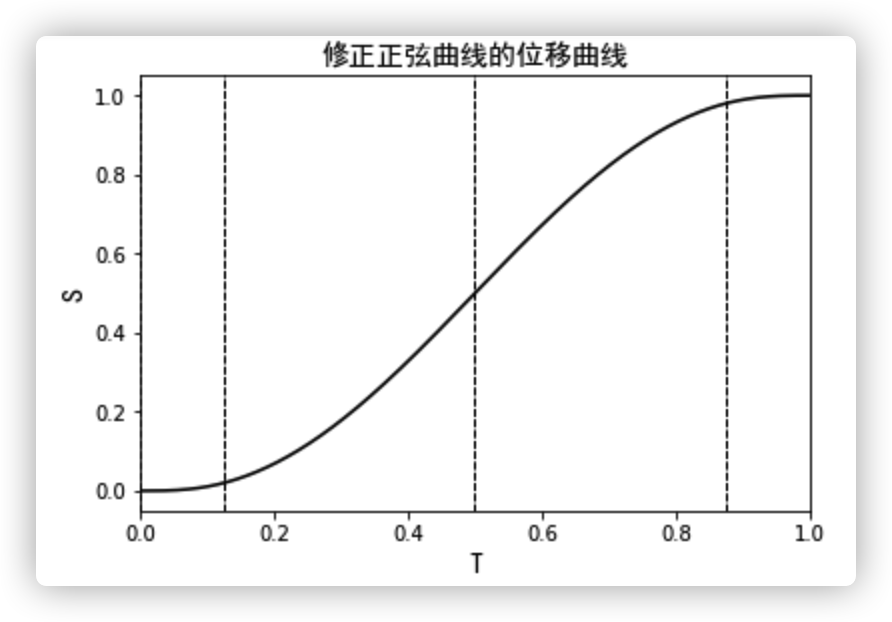
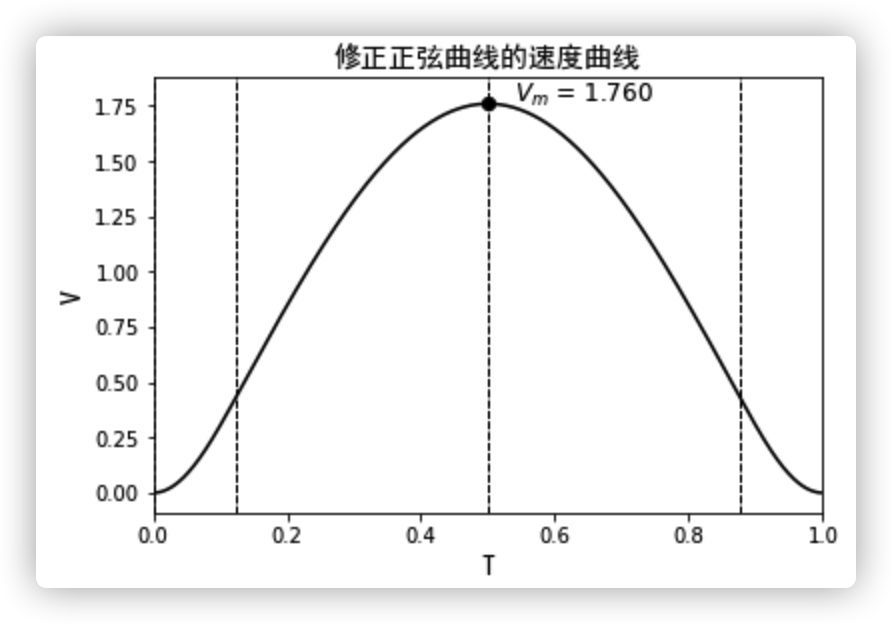
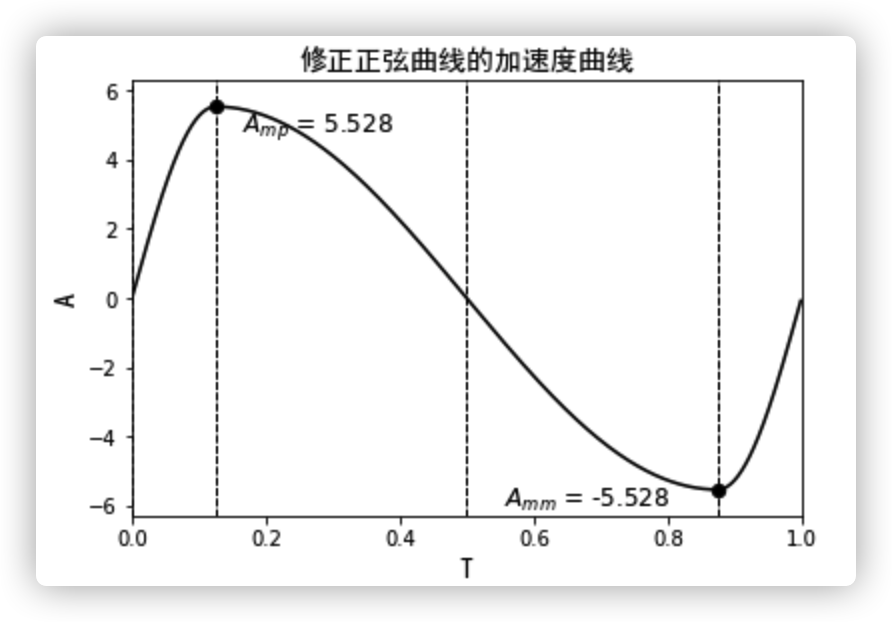
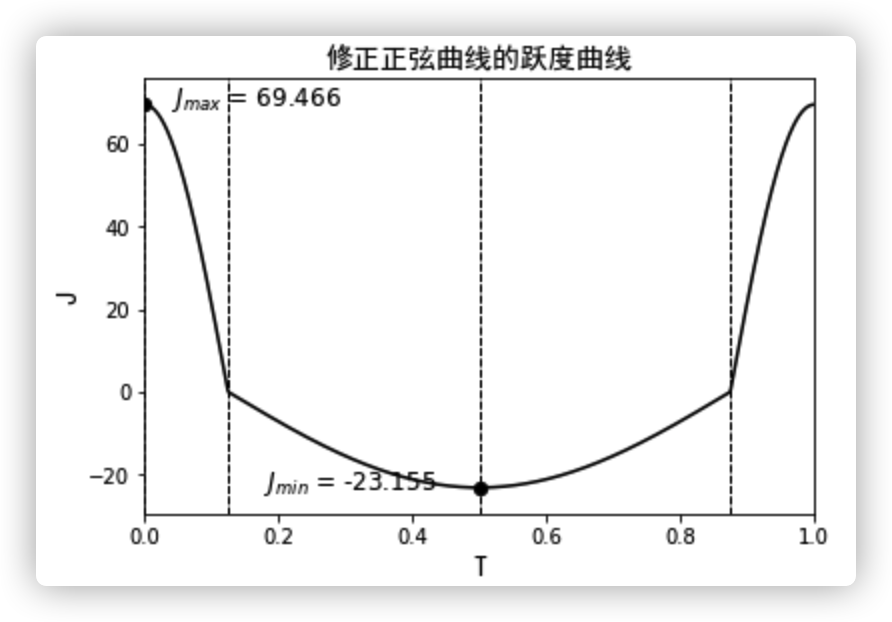
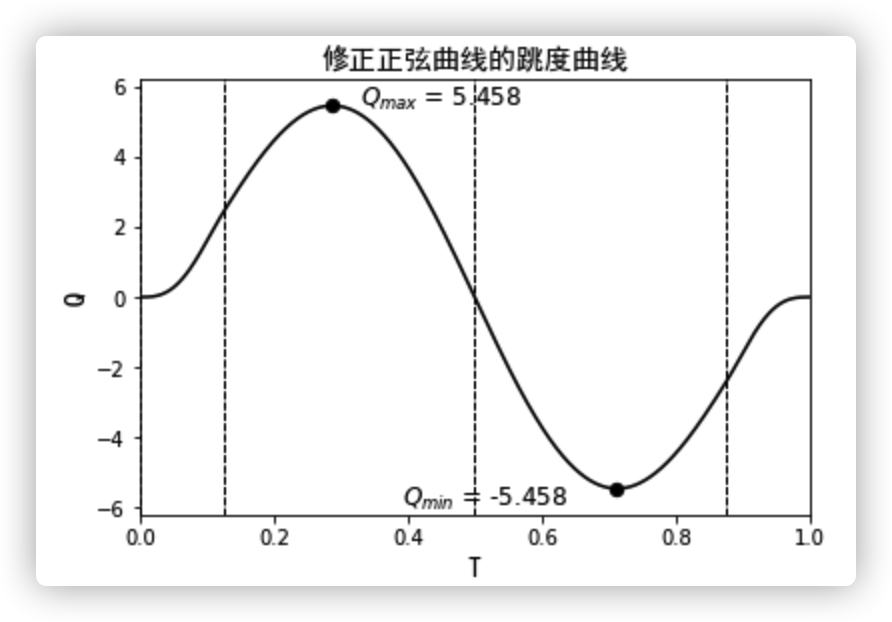
输出曲线的特性值为：

1
2
3
4
5
6
7
8
9
print('Vm =', np.max(V_axis))
print('Amp =', Amp_Amm[0])
print('Amm =', - Amp_Amm[1])
print('Jmax =', np.max(J_axis))
print('Jmin =', np.min(J_axis))
print('Qmax =', np.max(Q_axis))
print('Qmin =', np.min(Q_axis))
print('Rmax =', np.max(A_axis*S_axis))
print('Rmin =', np.min(A_axis*S_axis))

将无量纲时间转换为凸轮的转角：

1
2
T_axis_final = np.append(T_axis_final, T_axis*phi_list[0])
S_axis_final = np.append(S_axis_final, S_axis)

定义远休止阶段的运动曲线：

1
2
3
4
5
6
7
8
T_axis = np.array([])
S_axis = np.array([])
step = phi_list[1]*accur
T_axis = np.linspace(0, 1, step, endpoint=False)
S_axis = np.array([1]*step)

T_axis_final = np.append(T_axis_final, T_axis*phi_list[1] + phi_list[0])
S_axis_final = np.append(S_axis_final, S_axis)

同理，定义回程和近休止阶段的运动曲线，此处过程略。

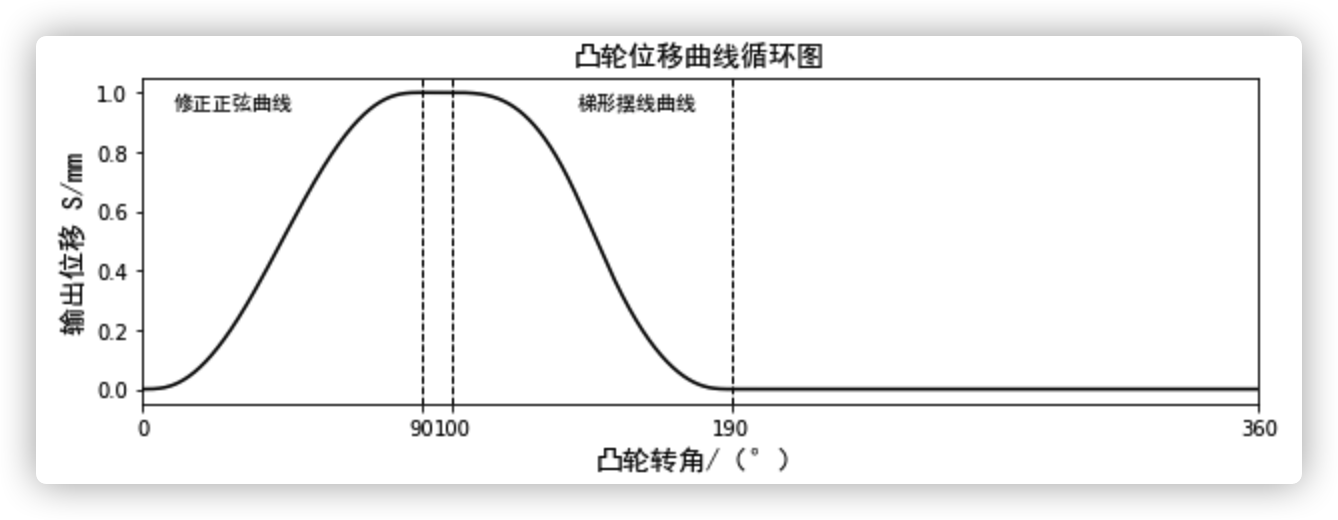
根据以上步骤得出的结果，最终可绘制出凸轮的位移循环图：

1
2
3
4
5
6
7
8
9
10
11
12
13
plt.figure(figsize=(10, 3))
plt.plot(T_axis_final, S_axis_final, color='k', linewidth=1.5)
plt.xticks([0, phi_list[0], phi_list[0] + phi_list[1], phi_list[0] + phi_list[1] + phi_list[2], 360])
plt.xlim(0, 360)
plt.title('凸轮位移曲线循环图', fontproperties="SimHei", fontsize=14)
plt.xlabel('凸轮转角/（°）',fontproperties='SimHei',fontsize=14)
plt.ylabel('输出位移 S/mm',fontproperties='SimHei',fontsize=14)
plt.axvline(x=phi_1, color='k', linewidth=1, linestyle='--')
plt.axvline(x=phi_2, color='k', linewidth=1, linestyle='--')
plt.axvline(x=phi_3, color='k', linewidth=1, linestyle='--')
plt.text(10, 0.95, curve_type[0], fontdict={'size': 12, 'color': 'k'}, fontproperties="SimHei")
plt.text(phi_3 - 50, 0.95, curve_type[1], fontdict={'size': 12, 'color': 'k'}, fontproperties="SimHei")
plt.show()

结果如下图所示：

6

输出 $S$ 值：

1
2
3
for i in range(len(T_axis_final)):
    if i%10 == 0:  # 输出角度为整数时的值
        print('%.1f°：%.6f'%(T_axis_final[i], S_axis_final[i]))

写在最后

这篇文章中的代码写于两年前，当时还开发了带有 UI 的通用简谐梯形组合凸轮曲线设计工具，可惜文件弄丢了。好在本文已覆盖了其背后逻辑运算的主要过程，希望对读者有所启发。

参考文献

［1］彭国勋，肖正杨.自动机械的凸轮机构设计［M］.北京：机械工业出版社，1990.

［2］刘昌祺，刘庆立，蔡昌蔚.自动机械凸轮机构实用设计手册［M］.北京：科学出版社，2013.

坚持原创技术分享，您的支持将鼓励我继续创作！